


Next: Final Remarks
Up: No Title
Previous: The Simple Model
The fictitious company whose supply chain is modeled here, was baptized the Perfect Minicomputer Corporation, giving the model its name: ``the PMC Model''. The design and implementation of the PMC Model is the major work of the thesis. The model is not a direct extension of the Simple Model from Chapter  , but the solutions found and experience acquired when implementing the Simple Model have been very useful when designing and implementing the PMC Model. Some parts, e.g. the production planning, rely on the logic used in Mujtaba [18]. The PMC Model, as it is seen in Figure
, but the solutions found and experience acquired when implementing the Simple Model have been very useful when designing and implementing the PMC Model. Some parts, e.g. the production planning, rely on the logic used in Mujtaba [18]. The PMC Model, as it is seen in Figure  (page
(page  ) is inspired by the ``typical global supply chain for the fabrication of a personal computers'' which is presented by Arntzen et al. [1].
) is inspired by the ``typical global supply chain for the fabrication of a personal computers'' which is presented by Arntzen et al. [1].
The overall objective of the thesis is translated into two main objectives when constructing the PMC Model:
- Design and implement, using COOL, a multi-echelon supply chain model, that will support both general and multi-plant coordination (as described in Section
 ). An aim of the implementation is to give EIL a more realistic supply chain demonstrator than the one currently in use.
). An aim of the implementation is to give EIL a more realistic supply chain demonstrator than the one currently in use. - Evaluate whether the multi-agent approach is well suitable for supply chain modeling. Are the assumptions made in motivation section (
 ) supported? Through simulations the aim is to: a) Investigating the performance of different coordination plans when unexpected events are simulated. b) Evaluate the way the model handles the pitfalls described in Section
) supported? Through simulations the aim is to: a) Investigating the performance of different coordination plans when unexpected events are simulated. b) Evaluate the way the model handles the pitfalls described in Section  .
.
The chapter is built up as follows: Section  presents the PMC Model, by describing the products and their composition, as well as entities (plants, inventories, distribution centers, suppliers, and customers) and processes. One may say that the section describes the supply chain as it emerges after strategic level decisions are made. Section
presents the PMC Model, by describing the products and their composition, as well as entities (plants, inventories, distribution centers, suppliers, and customers) and processes. One may say that the section describes the supply chain as it emerges after strategic level decisions are made. Section  describes the translation of the high level design in the prior section into a multi-agent system. Agents and conversation classes are identified, and processes are described in detail. Section
describes the translation of the high level design in the prior section into a multi-agent system. Agents and conversation classes are identified, and processes are described in detail. Section  describes the simulations that were run on the model and the results thereof.
describes the simulations that were run on the model and the results thereof.
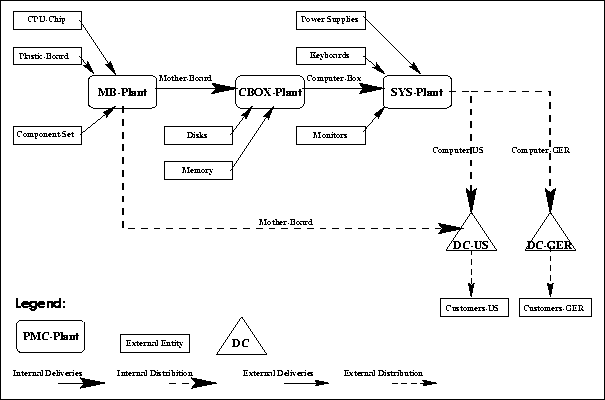
Figure: An overview of the PMC supply chain.
The Perfect Minicomputer Corp. (PMC) is a small supplier of mother boards and minicomputers situated in Toronto, Canada. The minicomputers are sold to customers in two markets, Canada/USA and Germany/Austria. In order to satisfy the different standards of keyboard and power supply in the two markets, the computers need to be slightly differentiated, and are regarded as two distinct products named Computer-US and Computer-GER. The mother boards is PMC's third product sold to external customers. The product name is simply Mother-Board. It is sold to the computer industry on the Canada/USA market. Figure  , showing the PMC Model supply chain, will be explained through this section.
, showing the PMC Model supply chain, will be explained through this section.
Table  shows the Bill of Materials for each of the products assembled by PMC. We see that Mother-Board is a part in the Computer-Box which is contained in the two computer products. The values of the products are simply the sum of the costs of its parts.
shows the Bill of Materials for each of the products assembled by PMC. We see that Mother-Board is a part in the Computer-Box which is contained in the two computer products. The values of the products are simply the sum of the costs of its parts.
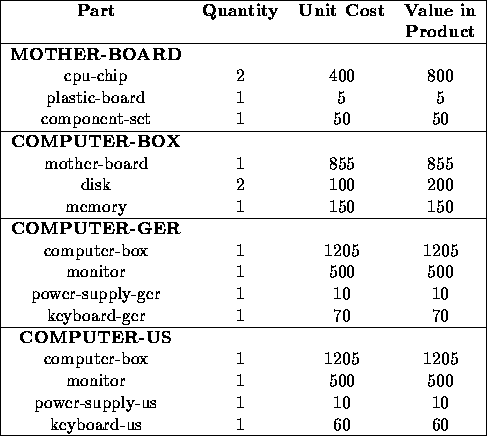
Table: Bill of Materials
PMC is a vertically integrated company. In addition to the assembly of the finished computer systems (computer, monitor and keyboard), and the mother boards used in the computer, it also assembles the computer boxes (without power supply) in a separate plant in Toronto. As can be seen in Figure  , PMC has three plants that will be referred to as system assembly (SYS-Plant), where the final assembly is done for the Computer-US and Computer-GER products, computer box assembly (CBOX-Plant), supplying the SYS-Plant with computer-boxes, and finally motherboard assembly (MB-Plant), supplying the CBOX-Plant, and shipping products to the Canada/USA market.
, PMC has three plants that will be referred to as system assembly (SYS-Plant), where the final assembly is done for the Computer-US and Computer-GER products, computer box assembly (CBOX-Plant), supplying the SYS-Plant with computer-boxes, and finally motherboard assembly (MB-Plant), supplying the CBOX-Plant, and shipping products to the Canada/USA market.
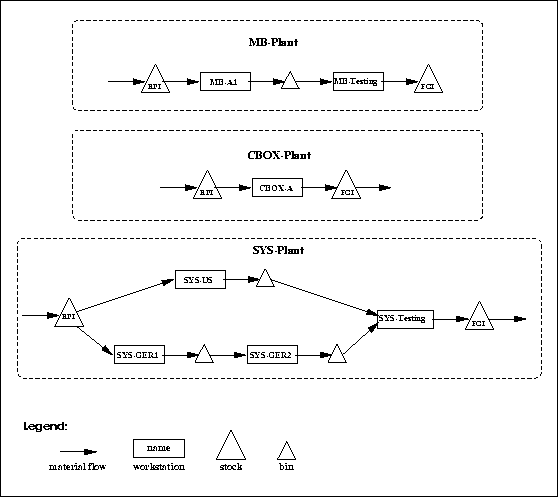
Figure: The plant architectures of the PMC Model.
Production will be simulated as pull production. Each plant is therefore modeled as a set of workstations, bins, and stocks, as is seen in Figure  .
.
The term workstations will be used for a production unit with the following attributes:
- a number of lines which defines the number of units that can be processed simultaneously in the workstation,
- a scrap rate (in percent) which defines the percent probability of a output unit being damaged, and therefore scrapped,
- a processing time for one unit of a given product, i.e. the time a unit stays in the workstation.
The production capacity of the work station is given by the number of lines times throughput rate (1 / processing time) minus expected scrap.
The storage areas between workstations are modeled as bins. Each bin has a maximum inventory level beyond which no products can be added. The sum of products in the workstations and bins give the current work in process inventory level (WIP).
A bin or stock from which a workstation takes material is called an input bin for the workstation. In this context the RPI will for instance be an input bin to the SYS-US workstation (see Fig.  ). The bin or stock to which a workstation adds materials is called the output bin of that workstation.
A workstation can have several input bins, but only one output bin.
). The bin or stock to which a workstation adds materials is called the output bin of that workstation.
A workstation can have several input bins, but only one output bin.
Each plant has two larger stocks, the raw product inventory (RPI) for incoming components or raw material, and the finished goods inventories (FGI) at the other end of production. The RPI has a safety stock level for each product. For the FGI's the safety stock level is set to 0 to avoid safety stocks both on the sender side (FGI) and the receiver's side (RPI or distribution center). Storage capacity is assumed infinite for all stocks.
Figure  shows that the MB-Plant has two work stations in a series, the first feeding the second. In the CBOX-Plant there is only one workstation. The SYS-Plant manufactures two products. The Computer-US is assembled in one workstation, and tested in the next, while the Computer-GER goes through two assembly stages before it is tested in the same testing station as Computer-US.
shows that the MB-Plant has two work stations in a series, the first feeding the second. In the CBOX-Plant there is only one workstation. The SYS-Plant manufactures two products. The Computer-US is assembled in one workstation, and tested in the next, while the Computer-GER goes through two assembly stages before it is tested in the same testing station as Computer-US.
As seen in Fig.  PMC also owns and operates their two distribution centers, one in Detroit for the Canada / USA market (DC-US), and one in Hamburg for Germany / Austria (DC-GER). All computers are distributed through these two distribution centers. All Mother-Boards sold to external customers are distributed through the Detroit distribution center.
PMC also owns and operates their two distribution centers, one in Detroit for the Canada / USA market (DC-US), and one in Hamburg for Germany / Austria (DC-GER). All computers are distributed through these two distribution centers. All Mother-Boards sold to external customers are distributed through the Detroit distribution center.
Distribution centers will have a safety stock level for each product. We assume infinite storage capacity in the distribution centers.
Table  shows suppliers, and their quoted lead time and prices for the parts. The prices are all converted to Canadian dollars. The model allows for normally distributed lead times with the quoted lead times as means, but this is not used in the simulations described in later sections.
shows suppliers, and their quoted lead time and prices for the parts. The prices are all converted to Canadian dollars. The model allows for normally distributed lead times with the quoted lead times as means, but this is not used in the simulations described in later sections.
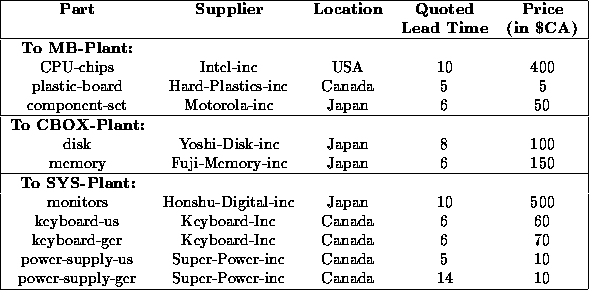
Table: Suppliers and Lead Times (note the difference in lead times for power-supply-us and power-supply-ger).
A transport has the following attributes:
- an origin,
- a destination,
- a carrier (boat or truck),
- an inventory (products and quantities),
- a duration (can be normally distributed).
Trucks have limited capacity, while boats are assumed to have unlimited capacity.
As seen from Figure  four classes of transports can be identified:
four classes of transports can be identified:
- from external supplier to plant (external delivery),
- from plant to plant (internal delivery),
- from plant to distribution center (internal distribution),
- from distribution center to customer (external distribution).
External deliveries are assumed to be handled by suppliers and are therefore not modeled. Internal deliveries are modeled as instantanious, and with unlimited capacity.
All transports to DC-US (internal distribution) are done by PMC's own trucks or, whenever necessary, added rental trucks. All transports to DC-GER (internal distribution) are done by boat. With the modest quantities manufactured by PMC, it is found reasonable to assume unlimited capacity.
All transports from distribution centers to customers (external distribution) are outsourced to a transportation company (WorldWide Transport inc.) both in Europe and North America. Unlimited capacity is assumed.
We identify three customer classes for computers in each market. What distiguishes these classes is the importance of the customers. In each market A customers are of highest importance, B customers below these, and the C customers of lowest importance. Since we do not identify separate customers, they have no other geographical address than their market. In the Canada/US market we also have industrial customers for the mother board. The middle letter of a customer class name is the importance indicator, and the last element in the name gives the market, e.g. the customer class Cust-A-US represents A customers in the Canada/US market.
The above describes the entities (suppliers, customers, plants, transporters, etc) as well as the products and parts of the model. This section deals with the processes necessary to receive materials, assemble these to form products, and ship the products to the next plant down the chain or to customers via distribution centers. Figure  gives a timeline for the processes through an ordinary week, without unexpected events.
gives a timeline for the processes through an ordinary week, without unexpected events.
As the week begins a demand forecast is issued, starting the week's production planning. The customer orders are modeled to come in as the production planing is done. Simultaneously the plants will order materials. Next material orders due this week will be delivered by the suppliers. At this point, we may say that it is 9 am Monday morning, and production is simulated till 5 pm Friday afternoon. The yield of the production will either be delivered to the next plant downstream or dispatched for a distribution center. Materials will arrive at distribution centers, and the the centers will fill orders from the backlog. Finally products sent transportation time weeks ago will arrive at customers.
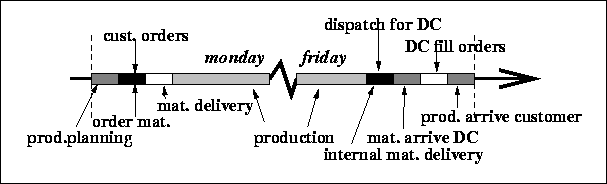
Figure: Weekly Processes in the Supply Chain.
The following is a more detailed description of the processes identified.
- Issuing the Order Forecast:
- With lead times for the parts of upto 15 weeks, several production stages and transport delays to and from distribution centers, material and production planning can not be done based on incoming customer orders. A demand forecast is necessary. This is the same principal as in the Simple Model (see Fig.
 , page
, page  ). Initially we give the demand forecast the same trapezoidal shape as in the Simple Model. This is shown in Figure
). Initially we give the demand forecast the same trapezoidal shape as in the Simple Model. This is shown in Figure  (page
(page  ). In the PMC Model one forecast is needed for each product in each market (where it is sold). The maximum forecast (V in Fig.
). In the PMC Model one forecast is needed for each product in each market (where it is sold). The maximum forecast (V in Fig.  ) for the computer products is set to 80 units per week, and for Mother-Boards V is set to 400. The length of the stable period. L, is set to 40 weeks (10 months).
) for the computer products is set to 80 units per week, and for Mother-Boards V is set to 400. The length of the stable period. L, is set to 40 weeks (10 months).
- Production Planning:
- Production planning is done based on the backlog and the order forecast. The principle of plans used in the Simple Model will also be employed here. Demand plans will be developed based on the order forecast and the backlog. The plans will flow upstream the supply chain. At each entity relevant knowledge will be added. On the way upstream the following knowledge should be included: all inventory levels and safety stock requirements, expected material deliveries, production capacities in the plants, and inventory in transit (plant to DC). As the plans reach the last upstream entity, they will return downstream as delivery plans. Based on the delivery plan of the preceding entity a plant can make its own delivery plan. A more detailed description of the material and production planning is left to the design section (
 ).
).
- Customer Ordering:
- Customers order a set ratio (A/F from the Simple Model) of the forecasted quantity for each week. Customer orders come in at the beginning of the week, but after the start of the production planning.
- Assigning Transportation Capacity Plant to DC:
- At the downstream end the delivery plans mentioned above will be the basis on which transportation capacity is assigned. Capacity will be assign on a origin to destination basis. When there is not enough company trucks, trucks will be rented, but this must be done at the beginning of the week.
- Materials Ordering and Delivery:
- Materials are ordered from external suppliers at the beginning of the week, and will also be delivered at the beginning of the week (before the start of production). Parts from internal supplier will be delivered at the end of the week (after the end of production). Delivered materials enter the RPI instantaniously and are thereby ready for assembly.
- Production:
- Production will be simulated as pull production. Each workstation has an output bin and one or more input bins. At each time unit products will be started in a workstation if: there are idle lines, all input bins contain enough parts, and the production goal for the product is not met. Output will be produced from a workstation if: a product unit is finished (has stayed in the workstation for atleast its production time), the output bin is not full, and the production goal for the product is not met.
- Plant to DC Dispatching:
- A plant will dispatch products for the distribution centers at the end of the week. The dispatched quantity of a product is that which is quoted in the delivery plan mentioned in the production planning section above. This is of course constrained by the inventory level in the FGI (equal to the week's production), and the transportation capacity assigned for the week.
- Plant to DC Transportation and Delivery:
-
Transportation times are defined as a function of origin, destination, and carrier. These may be uncertain (normally distributed). Shipments must be traced so that the arrival time is known. Upon delivery the products enter the distribution center inventory instantaneously, and are thereby ready for shipments to customers.
- DC Filling Orders:
- Customer orders are filled at end of the week, after the reception of shipments from plant (if any). The longest outstanding orders should be filled first, while for orders with same order date, A customers have priority over B and C customers, and B customers have priority over C customers. No order will be partially filled. If an order can not be filled, due to lack of material, it will wait till next week. Filled orders are dispatched the same week.
- DC to Customer Transport:
- Products arrive at customers at the end of the week, transportation time weeks after dispatching from DC.
This section will deal with the language dependent design of the model, i.e. forming the above described model as a multi-agent system implemented in COOL. As is already stated in Section  (page
(page  ) there are reasons to believe that a multi-agent approach gives good support to the designing process. Entities / functions and processes in the model are defined above. Agents will encapsulate entities and functions of the company. Agents are described in Section
) there are reasons to believe that a multi-agent approach gives good support to the designing process. Entities / functions and processes in the model are defined above. Agents will encapsulate entities and functions of the company. Agents are described in Section  .
.
A strength of the multi-agent approach is the ease of designing integrated systems with a high degree of coordination. This means that several agents will share the execution of some processes, e.g. production planning. Other processes naturally involve several agents, e.g. transfer of materials / products from one entity to another. Section  gives a detailed descriptions of the processes in the model.
gives a detailed descriptions of the processes in the model.
An agent is an entity encapsulating a set of functions or naturally occurring entities in the supply chain. To keep the agents relatively simple it is desirable to limit the number of functions encapsulated, usually to one.
As shown in Figure  , 40 agents are identified: 4 company wide agents, 2 DC agents, 22 agents in the plants, 2 customer agents, 8 supplier agents, the transport subcontractor, and finally the simulation agent. The following describes the agents and their roles.
, 40 agents are identified: 4 company wide agents, 2 DC agents, 22 agents in the plants, 2 customer agents, 8 supplier agents, the transport subcontractor, and finally the simulation agent. The following describes the agents and their roles.
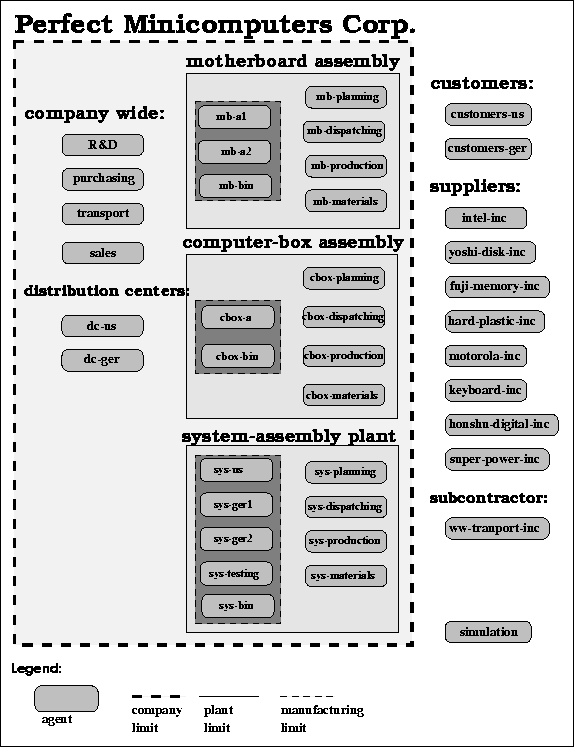
Figure: Presenting the agents in the PMC Model.
- Company wide agents:
- For functions that are not specific to a plant or a distribution center.
- Purchasing:
- the company's purchasing function. Selection and communication with external suppliers.
- Sales:
- marketing and sales functions. Makes demand forecast, and handles communication with customers.
- R&D:
- R&D function of the company. Owner of the Bill of Materials (in Table
 ).
).
- Transport:
- transportion function, handles transportation between plants and DC's.
- Distribution Centers:
- The agents of the distribution center.
- DC-US:
- all functions at the distribution center for the Canada/USA market.
- DC-GER:
- all funtions at the distribution center for the Germany/Austria market.
- Plant agents:
- Agents in each of the plants.
- a planning agent:
- planning functions. Handles production planning based on incoming demand plans and communication with other plants' planning agents.
- a production agent:
- handles production and work in process inventory, has knowledge of plant architecture (workstations and bins).
- a dispatching agent:
- handles finished goods inventory and all shipments from the plant.
- a materials agent:
- handles RPI, on-order data and all reception of materials.
- workstation agents:
- for each workstation, has knowledge of own capacities, handles events like machine breakdown.
- a bin agent:
- owner of inventory and max inventory data for the plant's bins.
- External Agents:
- Agents that are external to the company.
- customers-us:
- represents all customers in the Canada/USA market
- customers-ger:
- represents all customers in the Germany/Austria market
- suppliers agents:
- There is one agent for each of the suppliers in Table
 .
.
- ww-transport-inc:
- represents the subcontracted transportation company, transportation from distribution centers to customers.
The Simulation agent handles the progress of the simulation (start of new weeks) and the simulation of production.
The following gives a detailed description of the processes implemented. All processes are implemented by using one or several conversation classes. Tables  (page
(page  ) and
) and  (page
(page  ) give a list of the conversation classes and in which context (processes) they are used. The tables also show which agents use the conversation classes.
) give a list of the conversation classes and in which context (processes) they are used. The tables also show which agents use the conversation classes.
The thesis will not go into details on execution of conversation rules, in which order actions are performed, how this is implemented, and so forth. For detailed knowledge of this the reader is directed to the source code of the implementation in appendix  .
.
- Customer Ordering:
-
All customer orders will be calculated by the customer agents, and sent as a customer-order-set to the given sales agent. If the order is good (correct data structure and no logical mistakes) the sales agent gives the order an order number and adds it to the backlog. An acknowledgement message is sent to customers giving the order-number for reference purposes. Customers update their on-order data bases.
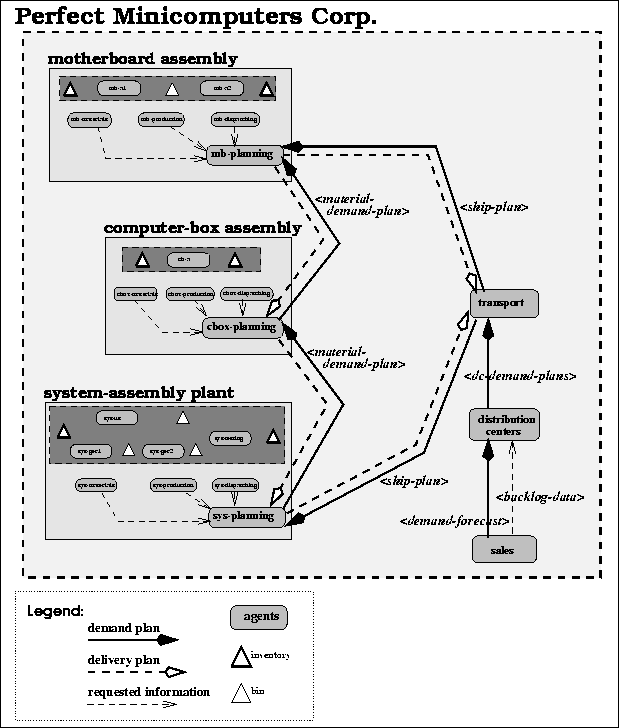
Figure: Production planning - General and Multi-Plant Coordination.
- Production Planning:
-
As is shown in Section
 the weekly production planning is a coordinated process, where both multi-plant and general coordination is used. Multi-plant coordination is done by the planning agents in each plant. As is shown in Figure
the weekly production planning is a coordinated process, where both multi-plant and general coordination is used. Multi-plant coordination is done by the planning agents in each plant. As is shown in Figure  , the downstream plant will communicate a demand to the upstream plant. The demand gives a shipment goal for the production planning of the upstream plant, who will communicate its capability to satisfy the demand to the downstream plant. These will be constraints on the production planning of the downstream plant.
, the downstream plant will communicate a demand to the upstream plant. The demand gives a shipment goal for the production planning of the upstream plant, who will communicate its capability to satisfy the demand to the downstream plant. These will be constraints on the production planning of the downstream plant.
Demands are communicated as a lists of quantities for this and future weeks. The lists are referred to as demand plans. Figure  shows how the demand plans flow upstream through the internal supply chain. The constraints flowing downstream are also lists of quantities, these being reffered to as delivery plans.
shows how the demand plans flow upstream through the internal supply chain. The constraints flowing downstream are also lists of quantities, these being reffered to as delivery plans.
The process starts with sales issuing a demand-forecast for each product in each market. The demand-forecast is a demand plan with quantities signifying the expected number of units order. The forecast is a-priori defined, and known by Sales. It is transmitted to the corresponding distribution centers.
The distribution centers will calculate its dc-demand-plan, which is a demand plan giving the quatities that the DC needs to satisfy actual and forecasted demand, and keep the inventory at safety stock levels. The safety stock levels are calculated in the same simple way that was described for the Simple Model (Section  ). Distribution centers keep safety stocks equal to 2 weeks of a 10 week's future average of forecasted demand. The demand plan is sent to the internal transport agent.
). Distribution centers keep safety stocks equal to 2 weeks of a 10 week's future average of forecasted demand. The demand plan is sent to the internal transport agent.
Transport makes a ship-plan for each plant, defining the quantity of each product that should be dispatched from the plant for a given DC in order to satify the dc-demand-plans (subtracted by quantities in transit) The ship-plans are distributed to the plants' planning agents.
The aim of a plant's planning agent is to convert the incoming ship-plan (if it has external customers) and materials-demand-plans from the next down-stream plants (if it has internal customers) to the plant's own materials-demand-plans, one for each internally supplied part. These are sent to the next upstream plants. A materials-demand-plan defines the number of units of a given product the plant needs in order to satisfy the total downstream demand. When calculating the materials-demand-plans the planning agent needs to request data from materials (for part availabilities), production (for WIP), and dispatching (for FGI).
The safety stock levels for internally supplied parts in the RPI, are determined by planning. The safety stock levels are calculated in the same simple way that was described for the Simple Model (Section  ). RPI safety for internally supplied parts is equal to 2 weeks of a 10 week's average of forecasted usage. Planning must also have knowledge of the workstations' capacities. This is knowledge derived from each workstation's attributes, and therefore it needs to be updated when changes occur in workstations.
). RPI safety for internally supplied parts is equal to 2 weeks of a 10 week's average of forecasted usage. Planning must also have knowledge of the workstations' capacities. This is knowledge derived from each workstation's attributes, and therefore it needs to be updated when changes occur in workstations.
There are several stages in the calculation of the materials-demand-plan. First a production-goal-plan is calculated. The calculation is based on total demand for each product, current FGI-levels, and safety stocks. Next step is to make the actual-build-plan.
The actual-build is the number of units of each product for which a plant will start production. It is the production-goal-plan modified for parts-availabilties and workstation capacities, i.e. a very simple production scheduling. The algorithm in this version of the model is very simple, dividing limited shared ressources equally among the products, i.e. so that an equal percentage of targetted production of each product is achieved. Externally supplied parts have unlimited availability beyond their lead times, since we assume that an unlimited number of units can be ordered each week. At this first stage, we assume unlimited availability of internally supplied parts for future weeks. The actual-build-plan gives the materials-demand-plan via the bill of materials (BOM).
The materials-demand-plans will move upstream till it meets a last planning agent in the internal supply chain. This agent will not calculate a materials-demand-plan, but rather go through the production-goal-plan and actual-build-plan stages to end with a delivery plan for each customer (next plants downstream, or transport for deliveries to DC) (If the plant has sufficient inventories and production capacities, the delivery-plans will be equal to the ship-plan and/or materials-demand-plans received.)
The delivery plan is communicated to next downstream planning agents for internal delivery and to transport for shipments to distribution centers. The downstream planning agent will use the incoming delivery plan(s) to modify its actual-build-plan. The availibility of internally supplied parts are now given by the received delivery plans. The new actual-build-plan gives the plant's delivery plan(s).
- Assigning Transportation Capacity Plant to DC:
- Done by Transport when all delivery plans for the week are received. This process is not of any importance in the following simulations.
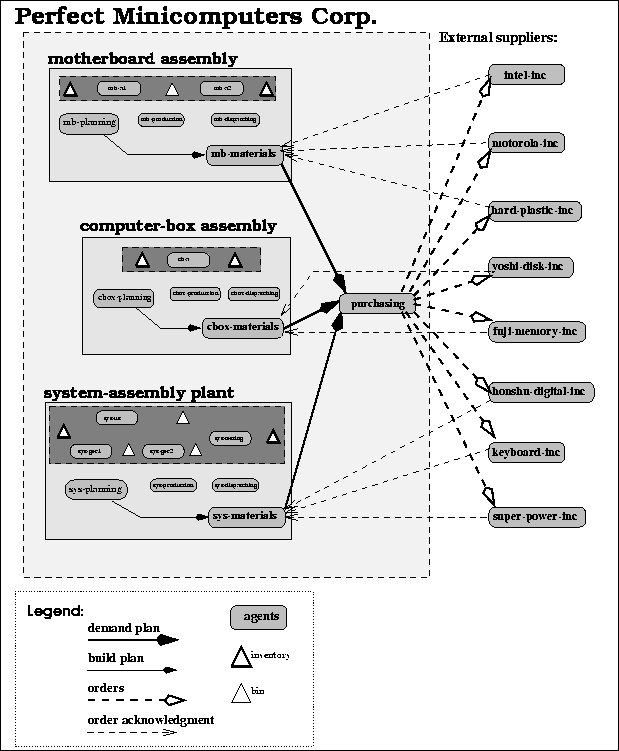
Figure: Information flow for materials ordering.
- Materials Ordering, Delivery, and Reception:
-
As is seen in Figure
 , materials agents are given the actual-build-plans by the planning agents. From these, via the BOM, and modified for RPI levels, RPI safety stock, and on-order, the agents can calculate a materials-order-plan for externally supplied parts. As shown in Fig.
, materials agents are given the actual-build-plans by the planning agents. From these, via the BOM, and modified for RPI levels, RPI safety stock, and on-order, the agents can calculate a materials-order-plan for externally supplied parts. As shown in Fig.  , these are demand plans. The RPI safety stocks for externally supplied parts are also equal to 2 weeks of average forecasted usage for the next 10 weeks (as for internally supplied parts). This is modified for parts with high variance of the supplier lead time. The variance of lead times are assumed to be known by the materials agents (derived from Purchasing's knowledge).
, these are demand plans. The RPI safety stocks for externally supplied parts are also equal to 2 weeks of average forecasted usage for the next 10 weeks (as for internally supplied parts). This is modified for parts with high variance of the supplier lead time. The variance of lead times are assumed to be known by the materials agents (derived from Purchasing's knowledge).
The plans are sent to Purchasing, who transforms them to marerials orders. The orders are gathered in order-sets and distributed to the supplier agents. The supplier agents will send acknowledgment messages to the materials agents (not Purchasing) with an order number assigned for reference purposes. (This is a time saving short-cut. Usually the acknowledgment would go via the purchasing agent.) The materials agents update their on-order data base.
Materials shipments arriving at the plants are modeled as a messages containing the orders arriving from the suppliers to the materials agents. The materials agents update inventory and on-order.
- Internal Materials Delivery:
-
Internal materials deliveries are modeled as messages from the supplying plant's dispatching agent to the customer plant's materials agent. The messages simply give products and quatities.
- Production:
-
The simulation agent handles the simulation of the production. All inventories, units in progress, and bins are updated by the simulation agent, thereby handling the flow of materials. Production is simulated with a time granularity of a day, allowing for events (e.g. workstation breakdown) to occur every morning. As a production week ends a message is sent to the production agents.
- Plant to DC:
-
- Dispatching:
-
In plants with external customers, the dispatching agent will dispatch products for transport to a DC. Dispatching sends a shipment-data message to transport. This gives destinations, products, and quantities.
- Transportation:
-
Upon receiving shipment data from dispatching, Transport will check if there is enough capacity assigned to transport the giving product quantities. This only applies when transportation is done by truck. When there is sufficient capacity assigned, Transport enters the shipments in the plant-dc-log, and answers dispatching with an accept message. Else, when Transport finds that the capacity of the assigned trucks is insufficient Transport assumes that dispatching wishes to ship the maximum amount possible. This is entered in the plant-dc-log, and a ``reduced''-message is returned to Dispatching giving the quantities that will be shipped. Dispatching updates FGI-levels based on the answer from Transport.
- Delivery:
-
Next, Transport will check plant-dc-log for shipments arriving at DC this week. Messages giving products and quantities, are sent to the distribution centers, and the transportation-log is updated. We assume no damage during transport.
- Reception:
-
When a distribution center receives the products arrived message the inventory is updated.
- DC to Customers:
-
- Dispatching:
-
The DC agents will fill orders in the backlog (requested from sales) based on the FGI-inventory. It will never fill an order partially. When a set of orders is filled, it is sent to Transport and sales. Sales updates the backlog.
- Transportation:
-
Next Transport updates the dc-customer-log, and checks the log for orders that arrive this week.
- Delivery and Reception:
- The arriving orders are deleted from the log, and sent to the appropriate customer agents, who then updates their on-order data bases.
- Data Recording:
-
Through the running of the model, statistical data is recorded. Each agent withing the corporation will record data within its field every week, building a data base. Table
 shows of data recording responsibilities in the PMC Model. At the end of the simulation the simulation agent will request the data from all agents (conversations request-stats-conv and send-stats-conv in table
shows of data recording responsibilities in the PMC Model. At the end of the simulation the simulation agent will request the data from all agents (conversations request-stats-conv and send-stats-conv in table  ), and save it to file for further analysis.
), and save it to file for further analysis.

Table: The PMC agents' data recording responsibilities.
Through the simulation various warning messages are written to a warning log. These can be browsed afterwards to complement the analysis of the statistical data. Warnings are written when: production planning shows that demand cannot be satisfied (bottleneck is identified), production plan is not met, there are stockouts in DC (DC cannot fill all orders in backlog) and orders are delivered late to customers.
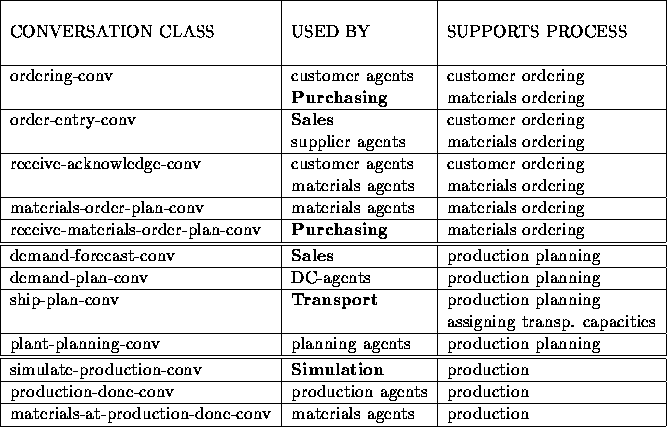
Table: Conversations and the processes they support, part 1.

Table: Conversations and the processes they support, part 2.
When running simulations on the PMC Model, a vast number of parameters can be varied, and the number of possible setups is infinite. In addition each simulation result in a great deal of data. It has therefore been important to limit the number of simulation, and have a clear focus when analysing the data produced. When choosing simulations and setups, the aim has been to highlight the objectives presented at the beginning of this chapter (Section  ).
).
Section  presents the results from simulating machine breakdown with various notification strategies, Section
presents the results from simulating machine breakdown with various notification strategies, Section  presents results from reducing information sharing in the production planning process, and Section
presents results from reducing information sharing in the production planning process, and Section  describes simulations with simple coordination protocols for quoting delivery dates. But first, Section
describes simulations with simple coordination protocols for quoting delivery dates. But first, Section  investigates the behaviour of the model and assesses its relevance as a supply chain model.
investigates the behaviour of the model and assesses its relevance as a supply chain model.
When starting to run simulations on the model, the first question to be asked is: Does this model actually behave like a supply chain? To try to verify the model, simulations where run where the ratio A/F was varied. The simulations where run without uncertainties
was varied. The simulations where run without uncertainties
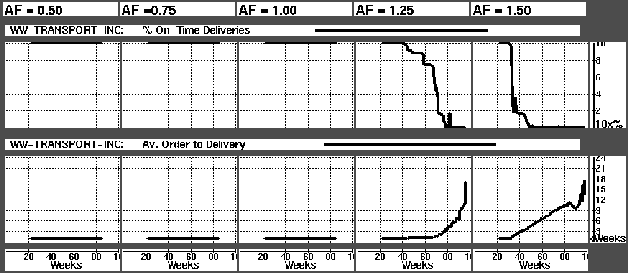
Figure: Graphs showing customer service as function of A/F.
Let us first concentrate on the issue of customer satisfaction. Figure  shows how the customer service decline as A/F increases. The upper row of graphs shows the development of the percent (of product values) that were delivered to customers on-time. On-time here is set to within a week, meaning that orders are shipped the week they are received. (Whether this is a realistic customer service target or not is irrelevant in this context.)
shows how the customer service decline as A/F increases. The upper row of graphs shows the development of the percent (of product values) that were delivered to customers on-time. On-time here is set to within a week, meaning that orders are shipped the week they are received. (Whether this is a realistic customer service target or not is irrelevant in this context.)
We see that as long as A/F is less or equal to 1 (the value of A/F is shown at the top), the company has no problem keeping a hundred percent customer service by satifying all orders on-time. When A/F grows above 1, however, and the demand thereby surpasses the forecasts, customer service becomes imperfect. For A/F = 1.25 we see that the curve starts falling in week 43, and hits 0% in week 79. When A/F is further increased to 1.5, 100% on-time delivery rate is only kept till week 32, and hits 0% already in week 49.
The lower line of graphs in Figure  shows the average time elapsed from customer orders arrive till they are delivered
shows the average time elapsed from customer orders arrive till they are delivered . These graphs show how critical the customer service failure is. Having 0% on-time delivery is not necessarily critical to the company if the average order to delivery time may be at 2 weeks. If order to delivery times are of upto 10-15 weeks above target, however, as we see when A/F is at 1.25 or 1.5, something is very wrong.
. These graphs show how critical the customer service failure is. Having 0% on-time delivery is not necessarily critical to the company if the average order to delivery time may be at 2 weeks. If order to delivery times are of upto 10-15 weeks above target, however, as we see when A/F is at 1.25 or 1.5, something is very wrong.
These results agree with the intuition that incorrect (too low) order forecasts will lead to imperfect customer service. The sales agent in the PMC Model is not equipped with the proper tools for adjusting its demand forecast as actual demand deviates from that which is forecasted. Production is thereby continuously planned on the basis of the incorrect forecasts. This again leads to incorrect ordering of materials.
It is important to note that there is finite production capacity in the model. The plants simply do not have the capacity to meet the demand when A/F = 1.5. In this case the imperfect customer satisfaction is a combination of insufficient capacity and production and materials planning based on incorrect demand forecasts.
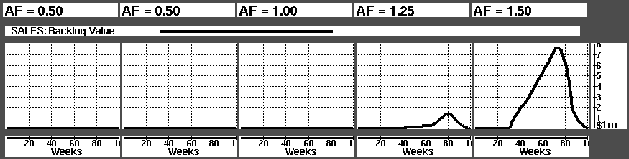
Figure: Graphs showing backlog value as function of A/F.
The backlog is also included in production planning. Indeed this is the reason the supply chain is able to eventually satisfy demand beyond that which has been forecasted. Figure  shows the backlog at the end of each week. We see that, as long as orders are shipped the week they come in, the backlog remains empty. When shipments are delayed, however, the backlog grows. As order volumes decrease towards the end of the product life cycles, the company is able to deliver more than the demand, and the backlog is reduced.
shows the backlog at the end of each week. We see that, as long as orders are shipped the week they come in, the backlog remains empty. When shipments are delayed, however, the backlog grows. As order volumes decrease towards the end of the product life cycles, the company is able to deliver more than the demand, and the backlog is reduced.
When the backlog grows and production goals are increased the response of the supply chain is slowed down by: the lead times on materials, the multi-stage production, and the transit times from plant to DC and DC to customers. (The response is further slowed by the limited capacity which prevent the plants from quickly catching up when the backlog grows large.)
The supply chain for the Computer-GER product is longer than that of the Computer-US. First the power supply used in Computer-GER has a lead time of 14 weeks, while that for Computer-US is only 5 weeks. Second the transit time from plant to DC-GER is 4 weeks, while for DC-US this is only one week. According to the discussions in Section  (Issues in Supply Chain Management), this should lead to less flexibility. The section states that customer service will suffer if inventories are not increased to ``buffer'' the lack of flexibility, as is the case here. Let us investigate the this.
(Issues in Supply Chain Management), this should lead to less flexibility. The section states that customer service will suffer if inventories are not increased to ``buffer'' the lack of flexibility, as is the case here. Let us investigate the this.
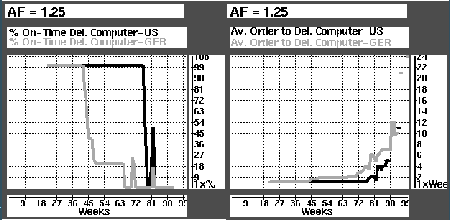
Figure: Graphs showing percent on-time deliveries and average time to delivery for Computer-GER and Computer-US when A/F is set to 1.25.
In Figure  the simulation with A/F = 1.25 has been isolated, and the two lines in the first graph window shows the percent of products delivered on-time for Computer-US (black line) and Computer-GER (gray line). We see that delivery of Computer-GER is sooner influenced by the incorrect demand forecast than is the case for Computer-US deliveries. For Computer-GER, on-time delivery drops from 100% already in week 42, while the supply chain for Computer-US tolerates the imperfect conditions until week 76. (A closer examination of the before mentioned warning log, shows that the Power-Supply-GER is indeed the bottleneck of Computer-GER production for weeks 34 to 69.)
the simulation with A/F = 1.25 has been isolated, and the two lines in the first graph window shows the percent of products delivered on-time for Computer-US (black line) and Computer-GER (gray line). We see that delivery of Computer-GER is sooner influenced by the incorrect demand forecast than is the case for Computer-US deliveries. For Computer-GER, on-time delivery drops from 100% already in week 42, while the supply chain for Computer-US tolerates the imperfect conditions until week 76. (A closer examination of the before mentioned warning log, shows that the Power-Supply-GER is indeed the bottleneck of Computer-GER production for weeks 34 to 69.)
The right hand graph window shows another side of customer service. The two lines of the graph, black for Computer-US and gray for Computer-GER, shows that the average time from order to delivery is consistently higher for Computer-GER.
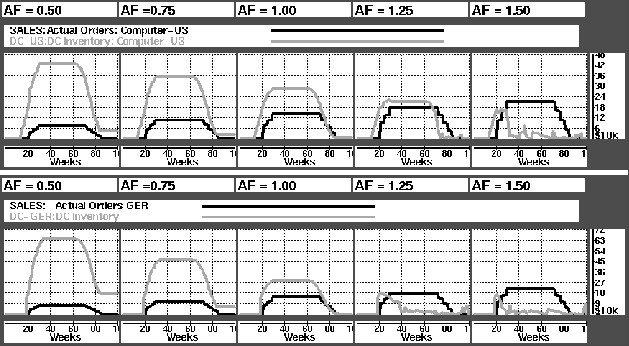
Figure: Graphs showing the DC inventories and demand for Computer-US and Computer-GER when the ratio A/F is varied.
Let us now examine the impact of varying values of A/F on the model's inventory levels. Figure  shows the DC inventory levels for Computer-US (gray line upper graphs) compared to demand (actual orders) for Computer-US (black line), and similarly DC inventory and demand for Computer-GER (lower line). First we take note of the case A/F = 1. This is the case where everything happens as expected. Looking at the inventory level, we see that it is approximately the double of the demand. This is not suprising since we remember that the DC safety stocks are 2 weeks of a 10 week's average of forecasted demand (which in this case is equal to the actual demand). The graphs merely confirm that inventory is kept at safety stock level at the end of each week. Since safety stock calculations are based on forecasted, not actual, order, the inventory level in the A/F = 1 graph shows the safety stock levels for all simulations.
shows the DC inventory levels for Computer-US (gray line upper graphs) compared to demand (actual orders) for Computer-US (black line), and similarly DC inventory and demand for Computer-GER (lower line). First we take note of the case A/F = 1. This is the case where everything happens as expected. Looking at the inventory level, we see that it is approximately the double of the demand. This is not suprising since we remember that the DC safety stocks are 2 weeks of a 10 week's average of forecasted demand (which in this case is equal to the actual demand). The graphs merely confirm that inventory is kept at safety stock level at the end of each week. Since safety stock calculations are based on forecasted, not actual, order, the inventory level in the A/F = 1 graph shows the safety stock levels for all simulations.
Moving beyond A/F = 1 to 1.25 and 1.5, we see a depletion of the distributions centers' inventory levels. At A/F = 1.25 we see that Computer-US levels are actually kept as planned, though slightly under targetted value (since more than expected is shipped every week ), until week 69. Computer-GER levels however fall as soon as the first orders come in. Again, this is due to the longer, less flexible supply chain for Computer-GER.
The reason for the eventual loss of Computer-US inventory is that production levels for Computer-GER slowly increase, leaving less of common ressources (workstation SYS-Testing, and common parts, see Table  ) to production of Computer-US. Study of the warning log shows that the Monitor, which is sharedby the two products, becomes the bottleneck ressource.
) to production of Computer-US. Study of the warning log shows that the Monitor, which is sharedby the two products, becomes the bottleneck ressource.
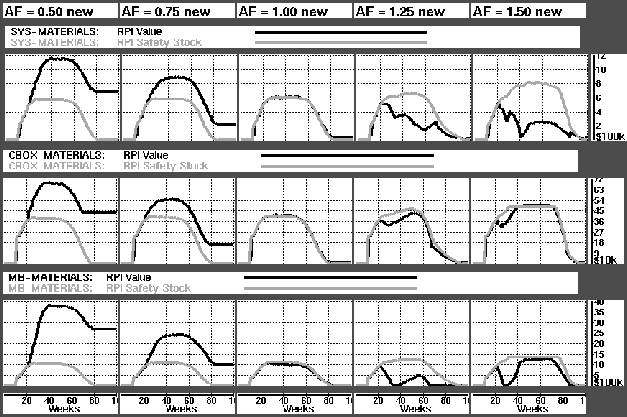
Figure: Graphs showing RPI levels compared to safety stock level as A/F vary.
When A/F is reduced we have seen that customer service levels are kept at 100%, but inventory levels are not kept as targeted. This leads to a high EOL write-off.
Let us turn to the other inventories of the PMC Model, the RPI's in the three plants. Figure  shows the development of the RPI levels
shows the development of the RPI levels . Again we see how a lower demand than expected results in high inventory levels and EOL write-off. Because of lead times for parts, we see the an increasing demand (A/F) temporarily depletes the inventories. As production is increased to satisfy the large amount of orders that are building up in the backlog, enough materials will be ordered to account for the increased production. Inventory levels will not only increase, they will in fact surpass those of a A/F = 1.
. Again we see how a lower demand than expected results in high inventory levels and EOL write-off. Because of lead times for parts, we see the an increasing demand (A/F) temporarily depletes the inventories. As production is increased to satisfy the large amount of orders that are building up in the backlog, enough materials will be ordered to account for the increased production. Inventory levels will not only increase, they will in fact surpass those of a A/F = 1.
The gray lines in the graphs show the safety stock levels. This is the targetted inventory, i.e. the inventory level that is aimed for in materials planning. It is calculated based on expected usage of each part. Therefore the targetted level decreases somewhat for A/F < 1, and increases for A/F > 1.
A probable advantage of increasing information sharing and coordination in the supply chain is the way unexpected events can be handled. Intuitively communicating agents should be able to enhance responsiveness to events such as strikes, machine breakdowns, cancelled ordered, late deliveries, and so on. This section presents simulations done with machine breakdowns. A machine breakdown in the model means a reduction of capacity of a workstation.
Breakdown is simulated in three workstations; MB-A1, CBOX-A, and SYS-Testing (see Figure  , page
, page  ). The breakdowns where simulated to occur Wednesday morning with these parameters:
). The breakdowns where simulated to occur Wednesday morning with these parameters:
- a breakdown week, the week the breakdown occors;
- a time of repair, a known time from breakdown to machine is repaired and normal capacity restored;
- a severity which is given as a percentage of lines that are out of function.
For the simulations presented below the breakdown week is week 35, time of repair is 12 weeks, and severity is set to 80% (90% for MB-A1) .
.
Two alternative coordination protocols for handling machine breakdown are implemented. The first solution is to do nothing. Knowledge of the breakdown remains with the workstation agent. The planning agent will continue to plan production as if capacity was unchanged. This setup will be referred to as ``without notification''. In the second case a conversation classes is added to the workstation agents, allowing these to notifying the production agent upon machine breakdown. If a production agent is notified, it will pass the message on to the plant's planning agent. The planning agent now knows of its plant's reduced production capacity, and will include this knowledge in the weekly production planning until the workstation is repaired. This setup will be referred to as ``with notification''.
The model presents no solutions to the problem of lost production when a workstation breaks down, and the decline in customer service is inevitable. There is in other words no significant difference in customer service for the two coordination scenarios. Let us therefore focus on the RPI levels. Intuitively we can assume that a plant's RPI levels will increase as production, and thereby the usage of parts, suddenly drops. The following describes the impact of the different breakdowns on the three plants' RPI levels.
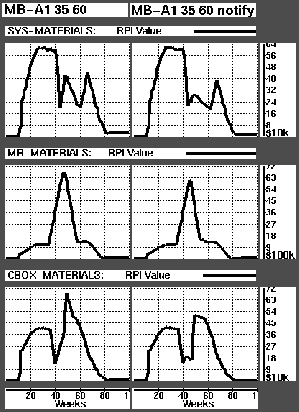
Figure: Graphs showing RPI levels when MB-A1's capacity is reduced by 90% between weeks 35 and 47.
Figure  shows how the breakdown affects the RPIs of the three plants. The graphs in the first column are taken from the simulation where the planning agent is not notified of the breakdown, while the second column shows the results of the notification strategy.
shows how the breakdown affects the RPIs of the three plants. The graphs in the first column are taken from the simulation where the planning agent is not notified of the breakdown, while the second column shows the results of the notification strategy.
As production drops in the MB-Plant all ordered materials will pile up in the plant's RPI. This is clearly shown in the middle row of graphs. Since materials orders cannot be cancelled this is inevitable. What can be done, however, is to stop ordering new materials. This is not done in the non-notification case, since the planning agent assumes full capacity, and plans production thereafter. The materials agent will order materials based on the wrong plan for future production. Where the planning agent is notified, it will plan the proper production level, and materials orders will drop as production drops. The figure clearly shows how the peak in value of the MB-Plant RPI diminish, both in magnitude and duration, by notifying planning of the breakdown.
The drop in supply of Mother-Boards leads to a drop in RPI value for the two downstream plants (since Mother-Boards constitute a high percentage of these values). This is shown in the upper and lower rows of the figure (the upper row for SYS-Plant, lower for CBOX-Plant). As we remember from the production planning process, there is already a built in coordination mechanism. The upstream plants will inform downstream plants of their future delivery-plan (see figure  , page
, page  ). If the planning agent of the MB-Plant gives the wrong delivery plans, as is the case for without notification, the downstream plants will order to much materials and the RPIs will grow. The right hand graphs show how this is avoided
). If the planning agent of the MB-Plant gives the wrong delivery plans, as is the case for without notification, the downstream plants will order to much materials and the RPIs will grow. The right hand graphs show how this is avoided by notifying the planning agent.
by notifying the planning agent.
Let us move one plant downstream. In this case breakdown is simulated in the CBOX-Plant's only workstation, CBOX-A. Figure  is composed the same way as Fig.
is composed the same way as Fig.  . Again we see how the planning agent's knowledge of the breakdown makes it capable of giving the correct production forecasts. These allow the materials agents to reduce materials orders at once a breakdown occurs. The very large improvement of the CBOX-Plant's RPI (lower row) is largely due to the reduction of Mother-Boards. A CBOX-Plant planning agent with accurate capacity knowledge is able to reduce intake of Mother-Boards within a week.
. Again we see how the planning agent's knowledge of the breakdown makes it capable of giving the correct production forecasts. These allow the materials agents to reduce materials orders at once a breakdown occurs. The very large improvement of the CBOX-Plant's RPI (lower row) is largely due to the reduction of Mother-Boards. A CBOX-Plant planning agent with accurate capacity knowledge is able to reduce intake of Mother-Boards within a week.
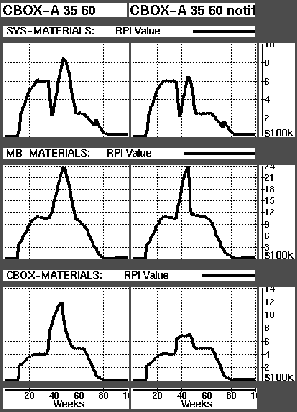
Figure: Graphs showing RPI levels when CBOX-A's capacity is reduced by 80% between week 35 and 47.
Due to this sudden reduction in intake of Mother-Boards in the case with notification, some of the inventory value gain from the CBOX-Plant is lost by a slightly higher peak in upstream inventory (MB-Plant). Still, averaging the MB-Plant inventory values over the 100 weeks of simulation, still shows an overall decrease when planning is notified.
In Figure  the upstream shift in RPI inventory mentioned above is more evident. In this case it is the very last workstation in the supply chain, SYS-Testing, that breaks down. The upper graph row shows a dramatic advantage of notifying planning: The SYS-Plant's average RPI value is reduced by 26%! For the two upstream RPIs, however, the effect is negative, i.e. the average RPI value is higher with notification than without. Though the upstream RPI build-up cancels out some of the gain in the SYS-Plant the overall result is positive. The average total RPI value is reduced by approximately 4%. The most important result however may be avoiding the sudden take-off of the SYS-Plant's stock. In the non-notification case the stock is more than tripled in the ten week period following the breakdown. The second case reduces the magnitude of the peek by almost half.
the upstream shift in RPI inventory mentioned above is more evident. In this case it is the very last workstation in the supply chain, SYS-Testing, that breaks down. The upper graph row shows a dramatic advantage of notifying planning: The SYS-Plant's average RPI value is reduced by 26%! For the two upstream RPIs, however, the effect is negative, i.e. the average RPI value is higher with notification than without. Though the upstream RPI build-up cancels out some of the gain in the SYS-Plant the overall result is positive. The average total RPI value is reduced by approximately 4%. The most important result however may be avoiding the sudden take-off of the SYS-Plant's stock. In the non-notification case the stock is more than tripled in the ten week period following the breakdown. The second case reduces the magnitude of the peek by almost half.
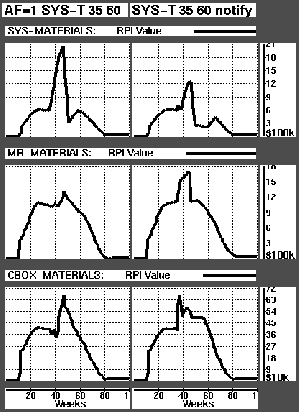
Figure: Graphs showing RPI levels when SYS-Testing's capacity is reduced by 80% between week 35 and 47.
Production planning is coordinated by having demand plans flow upstream the supply chain, while delivery plans flow downstream (see Fig.  , page
, page  ). The purpose of the delivery plans is to provide the downstream agents with knowledge of the state of the upstream supply chain. The downstream planning agent will know whether the upstream ability to deliver will constrain its future production. If this is the case, the plant may reduce the ordering of other parts, and thereby avoid filling its RPI with unused materials.
). The purpose of the delivery plans is to provide the downstream agents with knowledge of the state of the upstream supply chain. The downstream planning agent will know whether the upstream ability to deliver will constrain its future production. If this is the case, the plant may reduce the ordering of other parts, and thereby avoid filling its RPI with unused materials.
To verify that this information sharing effort worked as planned, simulations were run where the delivery plans were eliminated. This had little effect in a steady state situation, since downstream production is not constrained by that upstream. When we introduce machine breakdowns however, the effect is clear.
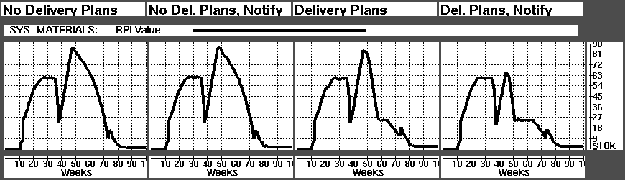
Figure: Graphs showing the impact of eliminating delivery plans from the model when breakdown is simulated in the CBOX-A workstation.
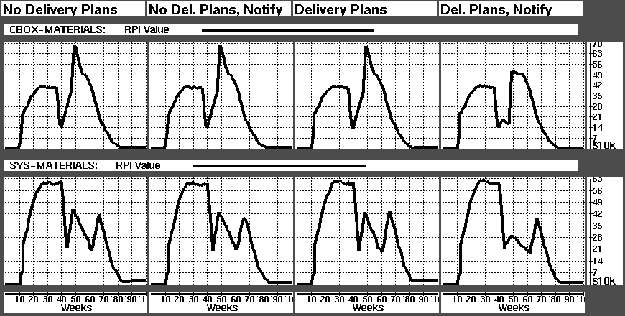
Figure: Graphs showing the impact of eliminating delivery plans from the model when breakdown is simulated in the MB-A1 workstation.
Figures  and
and  shows the impact of eliminating delivery plans from the model when breakdown is simulated in the CBOX-A and MB-A1 workstations respectively. Figure
shows the impact of eliminating delivery plans from the model when breakdown is simulated in the CBOX-A and MB-A1 workstations respectively. Figure  shows the SYS-Plant RPI levels, while Figure
shows the SYS-Plant RPI levels, while Figure  shows both CBOX-Plant and SYS-Plant RPIs. The first two graph windows in each row correspond to the case of no delivery plans. For the first graph windows the planning agent is not notified of the breakdown, while this is the case for the second graph window. We see that the notification has virtually no effect when delivery plans are not sent downstream. Intuitively this makes sense, since the notification knowledge is not shared with downstream planning agents.
shows both CBOX-Plant and SYS-Plant RPIs. The first two graph windows in each row correspond to the case of no delivery plans. For the first graph windows the planning agent is not notified of the breakdown, while this is the case for the second graph window. We see that the notification has virtually no effect when delivery plans are not sent downstream. Intuitively this makes sense, since the notification knowledge is not shared with downstream planning agents.
The last two graph windows of each row show the case were delivery plans are given . The first window without notification, the second with. In Figure
. The first window without notification, the second with. In Figure  the Computer-Box which is produced in CBOX-A is constraining to production in the SYS-Plant. Even for the case of no notification there is therefore a gain in RPI from the case of no delivery plans to the case of delivery plans. The gain is of approximately 16%. The gain for the case of with notification is as high as 26%!
the Computer-Box which is produced in CBOX-A is constraining to production in the SYS-Plant. Even for the case of no notification there is therefore a gain in RPI from the case of no delivery plans to the case of delivery plans. The gain is of approximately 16%. The gain for the case of with notification is as high as 26%!
For the breakdown of MB-A1 (Fig.  ), the advantage of sharing delivery information is only evident when notification is involved.
), the advantage of sharing delivery information is only evident when notification is involved.
A simple coordination structure was implemented for quoting delivery times to customers. The order processing is changed: Instead of simply adding incoming orders to the backlog and acknowledge reception, Sales will query the distribution centers for delivery times. If the inventory allows the orders to be filled (taking current backlog into account), the DC will answer Sales directly. If this is not the case, Transport will be asked by the DC.
Transort looks at the inventory in transit to DC's and the shipments promised from plants this week (in delivery plans from production planning). If there is still not enough to quote delivery times, the plants must be queried. The plants in question will give Transport an estimate of maximum shipments for the future. Based on this, Transport will quote the delivery times to DC. DC is now ready to answer Sales, and Sales sends acknowledgments to customers, this time including a quoted delivery date (week).
Simulations were run with different values of A/F (0.25, 0.5, 1.0, 1.25, and 1.5). Figure  shows the performance of the delivery time quoting compared to the on-time delivery percent. The black line shows percentage of on-time deliveries (delivered within a week). The gray line shows the percent that was quoted correctly, i.e. they were delivered in the week they where quoted.
shows the performance of the delivery time quoting compared to the on-time delivery percent. The black line shows percentage of on-time deliveries (delivered within a week). The gray line shows the percent that was quoted correctly, i.e. they were delivered in the week they where quoted.

Figure: Graphs showing % on-time deliveries and the % of delivered products that were correctly quoted.
We see from the graphs that there is no problems quoting delivery time as long as they are delivered on-time, as is the case for the first three simulations. As the ratio A/F and delivery times increases, however, the quoting of orders becomes uncertain (as the gray graph drops from 100% ).
).
The graph shows that at a certain moment the algorithms implemented can no longer quote corrrect lead times . No solution to this is implemented here. A suggestion would be to update the quoting of orders if they remain in the backlog after the quoted delivery date, thereby informing customers of late deliveries, and quoting a new delivery date. This would of course also be possible solution when uncertain events occur.
. No solution to this is implemented here. A suggestion would be to update the quoting of orders if they remain in the backlog after the quoted delivery date, thereby informing customers of late deliveries, and quoting a new delivery date. This would of course also be possible solution when uncertain events occur.
Based on the (limited) experience with the use of COOL to build a multi-agent system, the approach was found to facilitate the process of conceptualization. When entities and processes of the model had been identified, it was a straight forward process to encapsulate the entities in agents and the processes in conversation classes. More importantly the use of conversations was shown to be a powerful tool in designing coordination among the agents of the model.
The model is flexible. The simulations described above were done on different versions of the model. Based on an initial version, it was a small undertaking to alter or add conversation classes or agents, to form a new coordination setup.
Results from the simulations of machine breakdowns, show that the selection of coordination protocols has an impact on the performance of the system. Here, the sharing of relevant information was shown to be a key to reactive inventory management. By running simulations on different information sharing strategies we were able to quantify the loss caused by the lack of information sharing.
The notification of the planning agent in case of a breakdown was shown to enhance the overall RPI management of the supply chain. In a steady state, where no unforeseen events occur, simulations show that the there was not a high gain from the multi-plant coordination of production planning. In the case of a machine breakdown, however, the gain was shown to be substantial.
Lee and Billington [16] state that common pitfalls in inventory management are caused by; no supply chain metrics (no.1), inefficient information systems (no.4), and organizational barriers (no.7). The PMC Model lends support to the statement that information sharing, coordination, and thereby integration of the supply chain, is simplified by the use of a multi-agent system. In some cases the notification of the planning agent in the case of machine breakdown, proved to increase inventory levels at some plants while having the opposite effect in others. The model gave the opportunity to monitor the whole supply chain as one system, thereby allowing us to identify global gains, in spite of local loss.
The PMC Model is an example of distributed recording of data, which is communicated to a central agent, and formatted for analysis. This is a way to create relevant metrics for customer service, thereby avoiding Lee and Billington's second pitfall. Although it is not shown here, this is also a way to record uncertaities and develop high performing stocking policies (pitfalls 5 and 6). The simple coordination structure for quoting delivery times that was implemented, was not powerful enough to handle all unexpected conditions. However it did give another example of how agents can communicate to solve distributed tasks.



Next: Final Remarks
Up: No Title
Previous: The Simple Model
Rune Teigen
Tue May 27 17:50:58 EDT 1997
 , but the solutions found and experience acquired when implementing the Simple Model have been very useful when designing and implementing the PMC Model. Some parts, e.g. the production planning, rely on the logic used in Mujtaba [18]. The PMC Model, as it is seen in Figure
, but the solutions found and experience acquired when implementing the Simple Model have been very useful when designing and implementing the PMC Model. Some parts, e.g. the production planning, rely on the logic used in Mujtaba [18]. The PMC Model, as it is seen in Figure  (page
(page  ) is inspired by the ``typical global supply chain for the fabrication of a personal computers'' which is presented by Arntzen et al. [1].
) is inspired by the ``typical global supply chain for the fabrication of a personal computers'' which is presented by Arntzen et al. [1].






















